[ ]:

# Author : Dr. Davis Thomas Daniel
# Last updated : 03.09.2025

Data (1D)

Importing EPRpy

[1]:

import eprpy as epr

Loading data

[2]:

tempo = epr.load('tempo.DSC')

[3]:

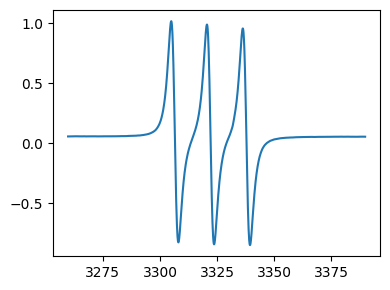
fig,ax=tempo.plot()
../_images/notebooks_examples_6_0.png 
[4]:

type(tempo) # tempo is an EprData object

[4]:

eprpy.loader.EprData

Plotting

  • Every EprData object has a plot method for making quick plots for inspection.

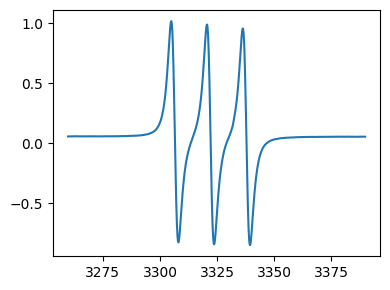
[5]:

fig,ax = tempo.plot()
../_images/notebooks_examples_10_0.png

Formatting plots

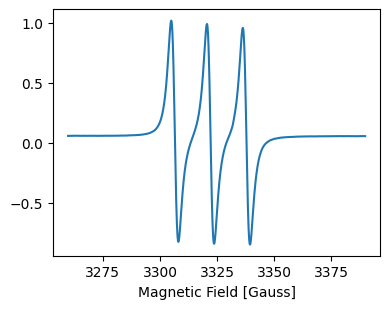
[6]:

ax.set_xlabel('Magnetic Field [Gauss]') # set x axis label
fig

[6]:
../_images/notebooks_examples_12_0.png

Use attributes directly to plot

  • Alternatively, plots can be made directly using matplotlib and EprData attributes with full control over formatting.

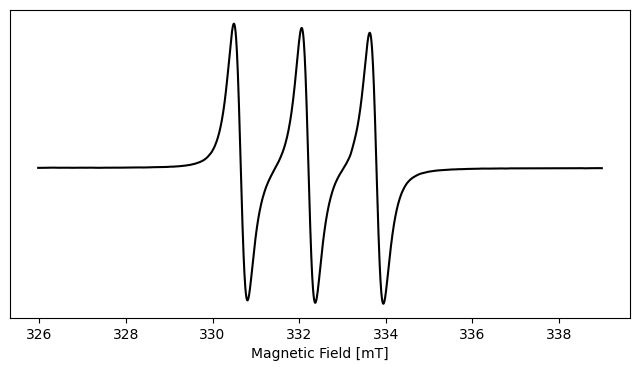
[7]:

import matplotlib.pyplot as plt
fig,ax = plt.subplots(figsize=(8,4))
ax.plot(tempo.x/10,tempo.data,color='black') # convert Gauss to mT
ax.set_xlabel('Magnetic Field [mT]') # set x axis label
_=ax.set_yticks([]) # hide intensity
../_images/notebooks_examples_15_0.png

Plot on the g axis

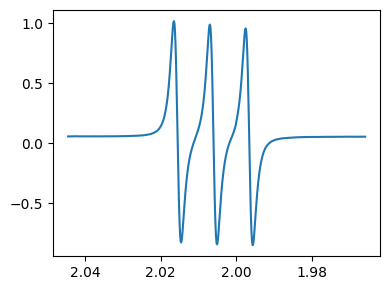
  • If the one of the axis is magnetic field, the g values are calculated internally and can be used for plotting as shown below.

[8]:

fig,ax = tempo.plot(g_scale=True)
../_images/notebooks_examples_18_0.png

Operations on Data

Scaling data

[9]:

# import EPRpy
import eprpy as epr

# load data
tempo = epr.load('tempo.DSC')

# scale between -1 and 1
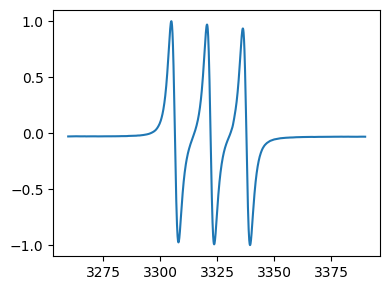
tempo_scaled = tempo.scale_between(-1,1)

print('After scaling : ')
fig,ax = tempo_scaled.plot()

After scaling :
../_images/notebooks_examples_21_1.png

Baseline correction

[12]:

# import EPRpy
import eprpy as epr

# load data
tempo = epr.load('tempo.DSC')

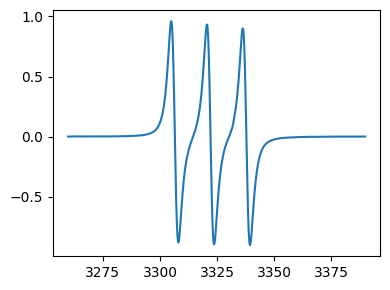
# linear baseline correction
tempo_bc = tempo.baseline_correct(npts=10) # default is linear baseline correction, npts is the data points used for baseline correction, here 10 points from the start and end of data
fig,ax = tempo_bc.plot()
../_images/notebooks_examples_23_0.png

Interactive baseline correction

[19]:

# import EPRpy
import eprpy as epr

# load data needs baseline correction
epr_data = epr.load('data_for_bc.DTA')

# plot the data without bc
fig,ax  = epr_data.plot()
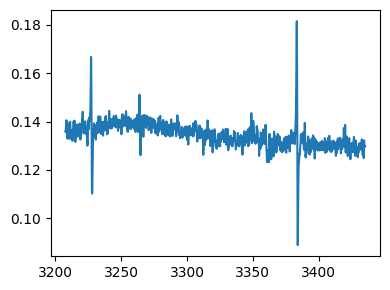
../_images/notebooks_examples_25_0.png

  • As an example, we baseline correct the spectrum by using a 3° polynomial. For baseline calculation, the points are picked interactively.

[20]:

# if you are using a jupyter notebook, switch to qt backend for matplotlib
#%matplotlib qt

# to switch back to inline mode:
#%matplotlib inline

[ ]:

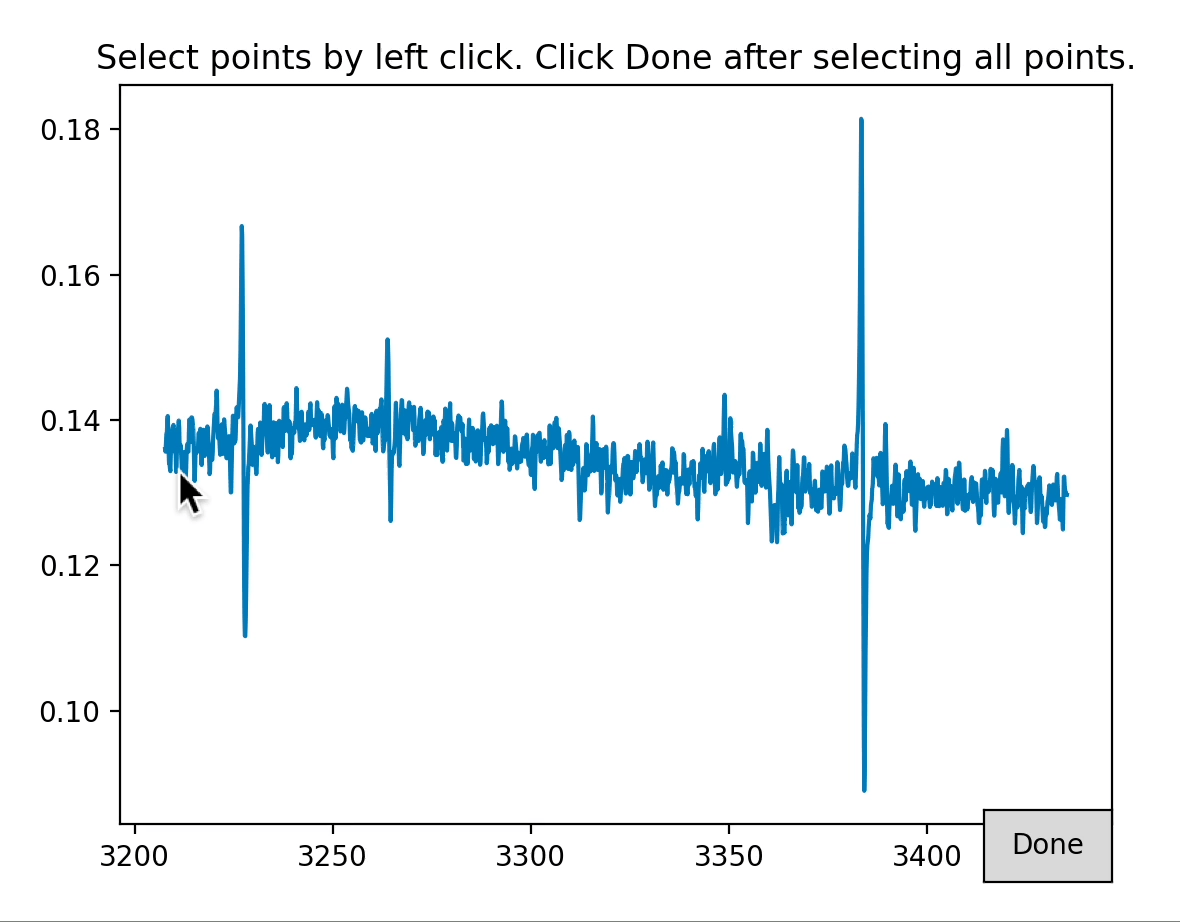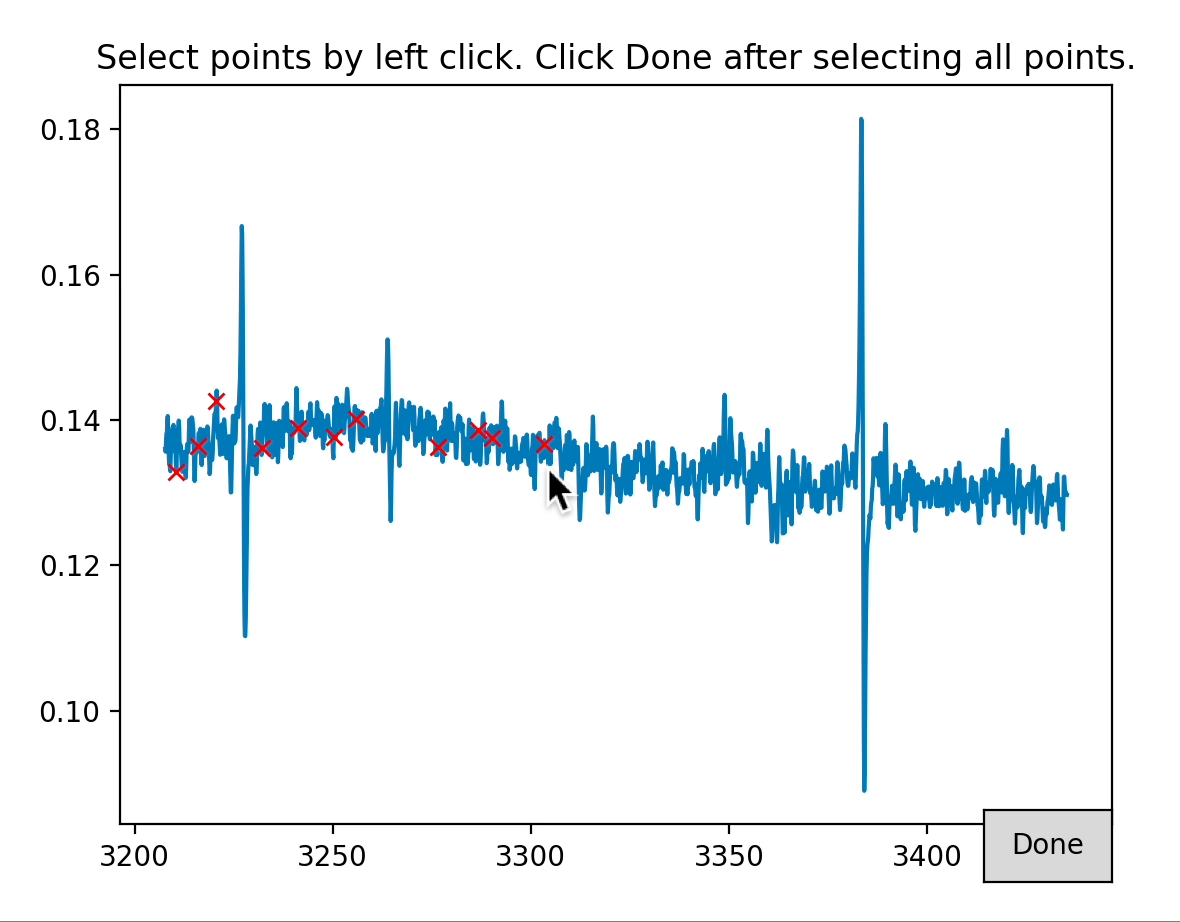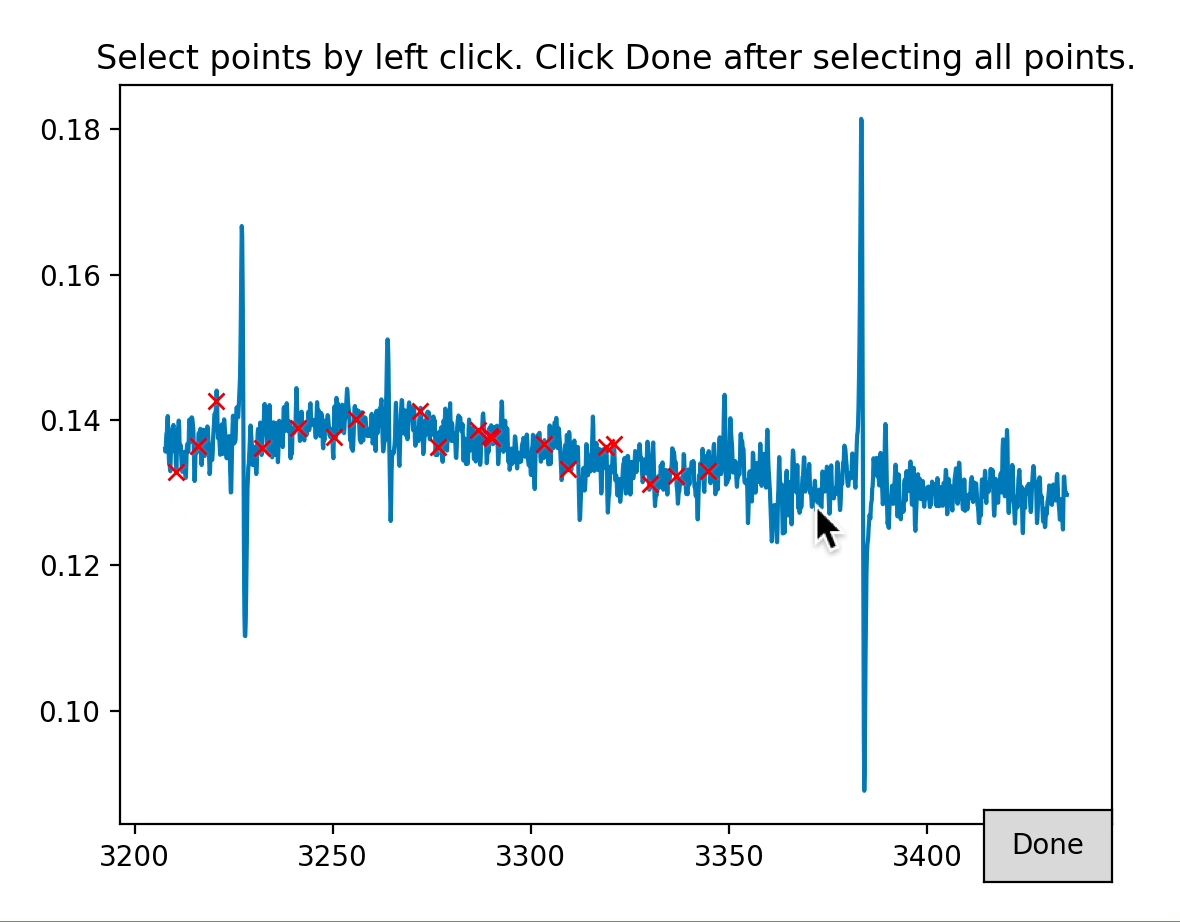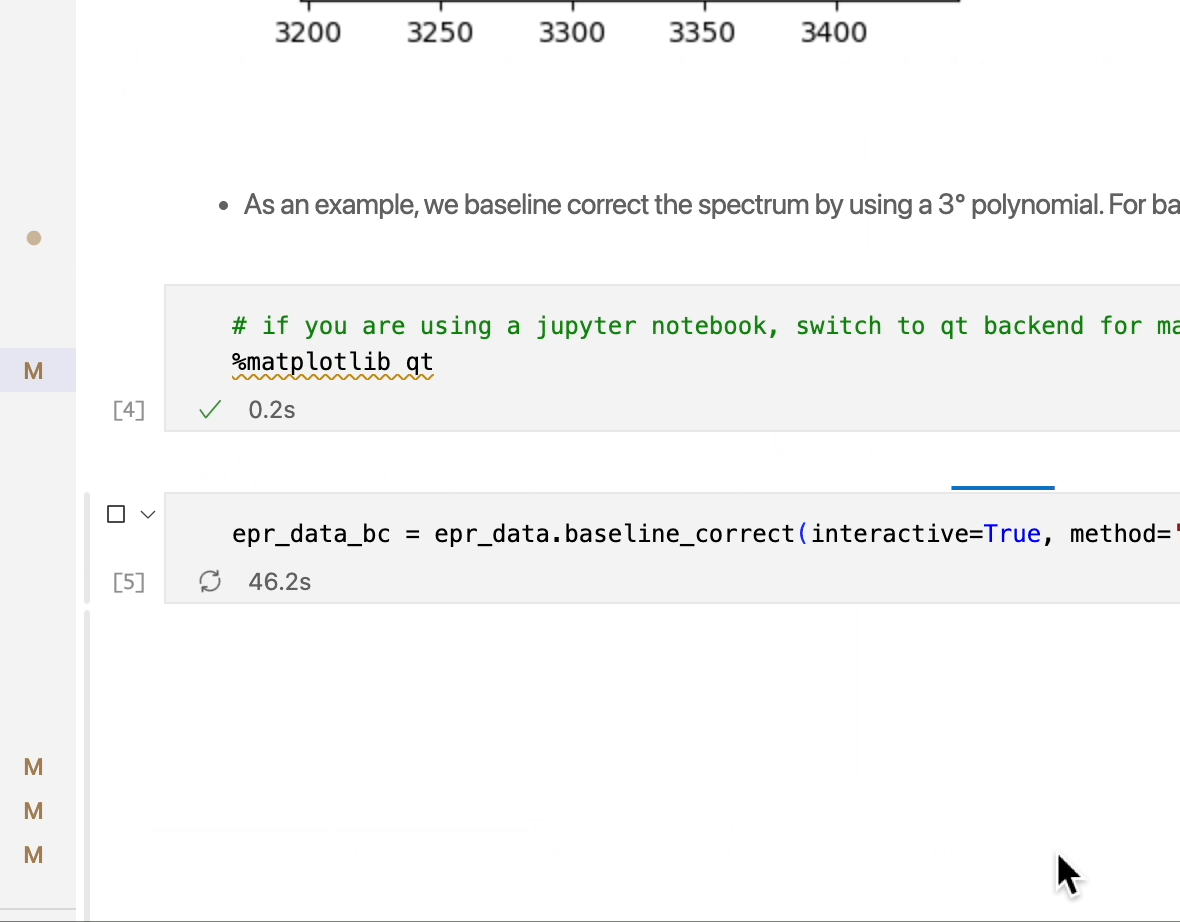
epr_data_bc = epr_data.baseline_correct(interactive=True, method='polynomial',order=3)

interactive_bc

[22]:

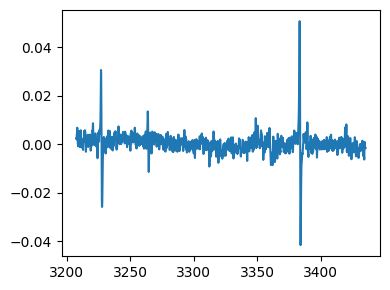
# plot the baseline corrected spectra
fig,ax = epr_data_bc.plot()
../_images/notebooks_examples_30_0.png

Computing integrals

[24]:

# import EPRpy
import eprpy as epr

# load data
tempo = epr.load('tempo.DSC')

# baseline correction and integration
tempo_proc = tempo.baseline_correct(npts=10)
tempo_proc = tempo_proc.integral()

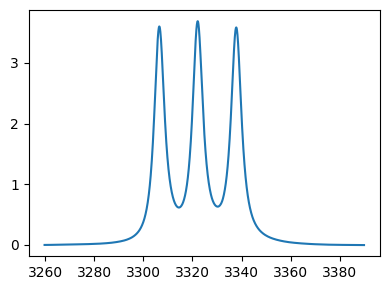
# plot the absorption signal
fig,ax = tempo_proc.plot()
../_images/notebooks_examples_32_0.png

Selecting a region

  • For this example, we assume that the desired region is the low field hyperfine line.

[25]:

# import EPRpy
import eprpy as epr

# load data
tempo = epr.load('tempo.DSC')

# Plot the data using an array with unity spacing to find corresponding indices
import matplotlib.pyplot as plt
print('Full spectrum : ')
_=plt.plot(tempo.data)

# make a new EprData object corresponding to the desired region
tempo_region = tempo.select_region(range(550,850)) # indices from 0 to 900

Full spectrum :
../_images/notebooks_examples_35_1.png 
[26]:

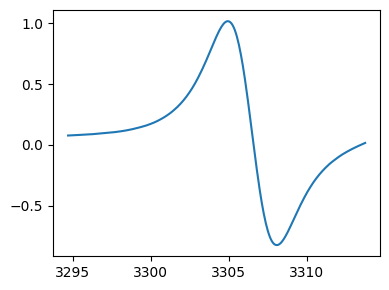
# selected region, note that the the new EprData object tempo_region only has the data corresponding to this region
print('Selected region : ')
fig,ax = tempo_region.plot()

Selected region :
../_images/notebooks_examples_36_1.png

History of data operations

EPRpy allows for keeping a log of data operations done on an EprData object, as long as in-built functions are used.

[27]:

# import EPRpy
import eprpy as epr

# load data
tempo = epr.load('tempo.DSC')

# do some operations
tempo_proc1 = tempo.scale_between(-1,1)
tempo_proc2 = tempo_proc1.baseline_correct(npts=10)
tempo_proc3 = tempo_proc2.integral()

Access history

  • Each EprData object stores history of all data operations and the corresponding EprData object in a list of lists. The first item in each list is the description of the data operation and the second item is the corresponding EprData object.

[28]:

tempo_proc3.history

[28]:

[['2025-09-03 17:07:52.029357 : Data loaded from tempo.DSC.',
  <eprpy.loader.EprData at 0x13eee9b50>],
 ['2025-09-03 17:07:52.030758 : Data scaled between -1 and 1.',
  <eprpy.loader.EprData at 0x13eee9c40>],
 ['2025-09-03 17:07:52.032316 : Baseline corrected',
  <eprpy.loader.EprData at 0x13eee9ca0>],
 ['2025-09-03 17:07:52.034752 : Integral calculated',
  <eprpy.loader.EprData at 0x13eed4110>]]

  • To plot or access a specific EprData from the history, simply use indexing. For instance, to view the original data again, plot the first item in history:

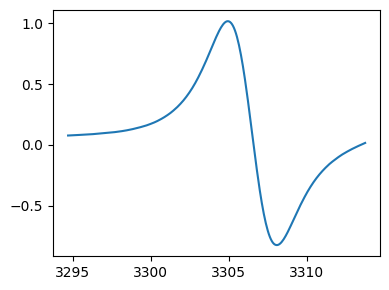
[29]:

print(tempo_proc3.history[0][0])
fig,ax = tempo_proc3.history[0][1].plot()

2025-09-03 17:07:52.029357 : Data loaded from tempo.DSC.
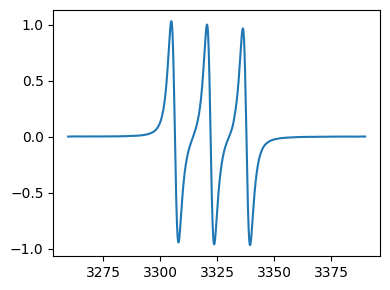
../_images/notebooks_examples_44_1.png 
[30]:

print(tempo_proc3.history[2][0])
fig,ax = tempo_proc3.history[2][1].plot()

2025-09-03 17:07:52.032316 : Baseline corrected
../_images/notebooks_examples_45_1.png

Data (2D)

## Importing EPRpy

[31]:

import eprpy as epr

Loading data

[32]:

## TEMPO radical monitored as a function of time
## For some 2D datasets, a .GF file must also be present in the same folder.
tempo2d = epr.load('tempo_time.DSC')

[33]:

tempo2d.data.shape # this dataset corresponds to 48 time values (tempo2d.y) and 1024 field points (tempo2d.x)

[33]:

(48, 1024)

[34]:

tempo2d.y # time in seconds

[34]:

array([    0.  ,  1533.1 ,  3065.64,  4598.25,  6130.95,  7663.46,
        9196.02, 10728.54, 12261.1 , 13793.49, 15326.14, 16858.79,
       18391.58, 19924.32, 21457.01, 22989.5 , 24521.66, 26054.41,
       27586.94, 29119.64, 30652.35, 32184.94, 33717.75, 35250.49,
       36783.1 , 38315.81, 39848.56, 41381.3 , 42913.97, 44446.53,
       45978.94, 47511.65, 49044.47, 50576.93, 52109.66, 53642.3 ,
       55175.05, 56707.73, 58240.42, 59773.14, 61305.37, 62837.76,
       64370.26, 65902.73, 67435.12, 68967.26, 70499.68, 72031.99],
      dtype='>f8')

[35]:

tempo2d.x # field values in Gauss

[35]:

array([3273.65      , 3273.74658203, 3273.84316406, ..., 3372.26025394,
       3372.35683597, 3372.453418  ], shape=(1024,))

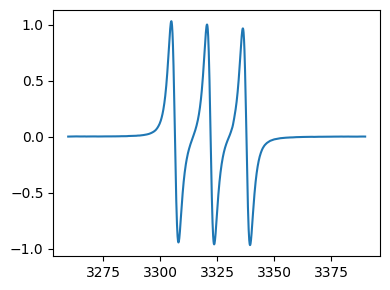
Plotting

Stacked plot

[36]:

fig,ax = tempo2d.plot(spacing=5)
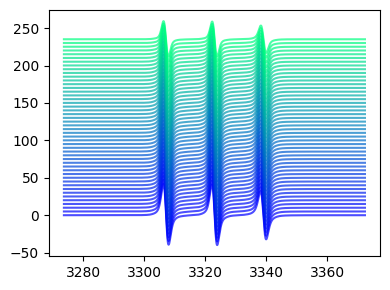
../_images/notebooks_examples_56_0.png

Superimposed plot

[37]:

fig,ax = tempo2d.plot(plot_type='superimposed')
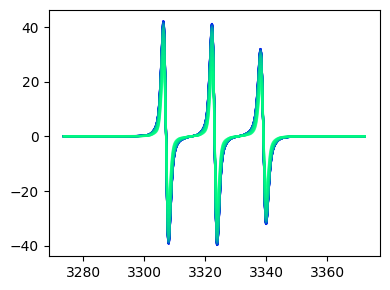
../_images/notebooks_examples_58_0.png

Pseudocolor plots

[38]:

fig,ax = tempo2d.plot(plot_type='pcolor')
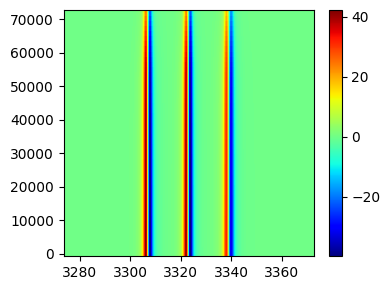
../_images/notebooks_examples_60_0.png

Surface 3D plot

[39]:

fig,ax = tempo2d.plot(plot_type='surf')
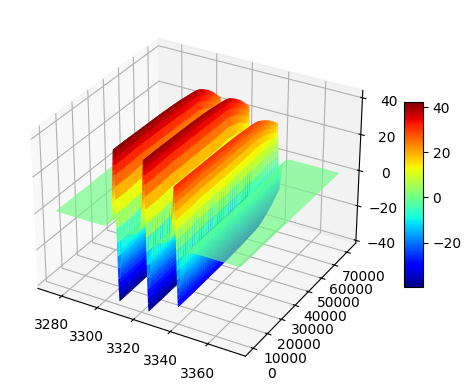
../_images/notebooks_examples_62_0.png

Workflows

HYSCORE

[1]:

import eprpy as epr

[2]:

tempo_hyscore = epr.load("tempo_hyscore.DSC")

Plot the time-domain data

[3]:

_=tempo_hyscore.plot(plot_type="pcolor")
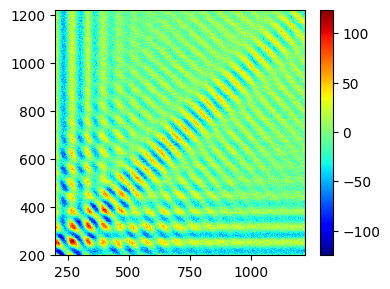
../_images/notebooks_examples_68_0.png

Process using HYSCORE workflow

[4]:

hyscore_proc = tempo_hyscore.workflow(zf=1024) # zero fill with 1024 points

[5]:

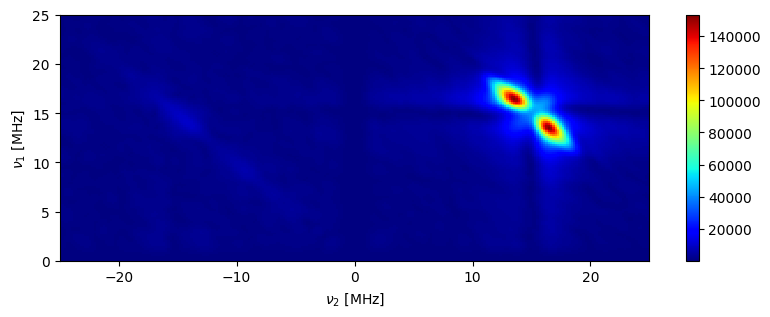
fig,ax=hyscore_proc.plot(plot_type="pcolor")
fig.set_size_inches((10,3))
ax.set_ylim((0,25))
ax.set_xlim((-25,25))
ax.set_xlabel(r"$\nu_{2}$"+" [MHz]")
_=ax.set_ylabel(r"$\nu_{1}$"+" [MHz]")
../_images/notebooks_examples_71_0.png 
[6]:

# Processing workflows can be controlled by other parameters
# zero fill with 1024 points
# symmetrise the final spectrum along the diagonal
# change polynomila order for background correction to 4
# verbose=True for printing progress

hyscore_proc1 = tempo_hyscore.workflow(zf=1024,symmetrise="diag",poly_order=4,verbose=True)

Starting HYSCORE workflow...
Baseline correction in dimension 1 with polynomial of order 4...
Baseline correction in dimension 2 with polynomial of order 4...
Applying Hamming window in dimension 1...
Applying Hamming window in dimension 2...
Zero filling 1024 points dimension 1 and 2...
Generating frequency axes...
2D Fourier transformation...
Symmetrising along the diagonal and the antidiagonal...
Completed in 0.12 seconds.

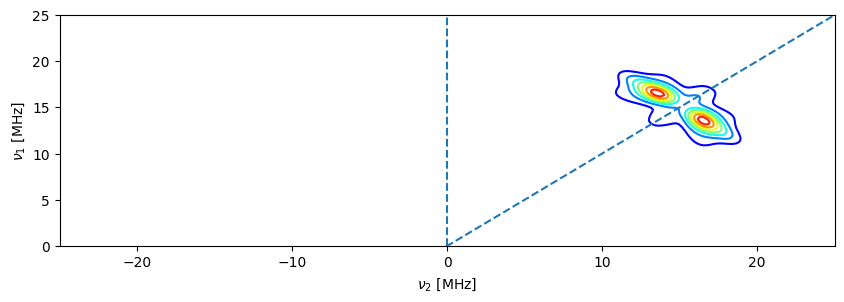
[7]:

# you can also plot manually using matplotlib and format to your liking

import matplotlib.pyplot as plt
fig,ax = plt.subplots(figsize=(10,3))
ax.contour(hyscore_proc1.data_dict["frequency_axis1"],hyscore_proc1.data_dict["frequency_axis2"],hyscore_proc1.data,cmap="jet")
ax.set_ylim((0,25))
ax.set_xlim((-25,25))
ax.vlines(0,ymax=25,ymin=0,linestyles="dashed")
ax.plot(hyscore_proc1.x,hyscore_proc1.x,linestyle="dashed")
ax.set_xlabel(r"$\nu_{2}$"+" [MHz]")
_=ax.set_ylabel(r"$\nu_{1}$"+" [MHz]")
../_images/notebooks_examples_73_0.png 
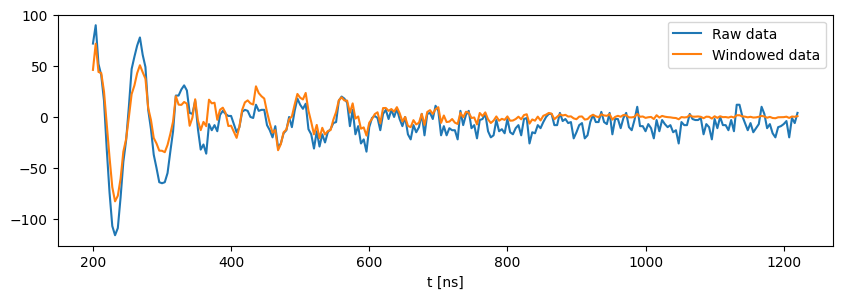
[8]:

# you can also plot other arrays from any step of the processing pipeline
# here the raw time domain data before and after applying a window function is visualized

import matplotlib.pyplot as plt
fig,ax = plt.subplots(figsize=(10,3))

ax.plot(hyscore_proc1.data_dict["x_raw"],hyscore_proc1.data_dict["raw_data"].real[0],label="Raw data")
ax.plot(hyscore_proc1.data_dict["x_raw"],hyscore_proc1.data_dict["bc_w_data"][0],label="Windowed data")
ax.set_xlabel("t [ns]")
_=ax.legend()
../_images/notebooks_examples_74_0.png

2P ESEEM

[9]:

tempo_eseem = epr.load("tempo_eseem.DSC")

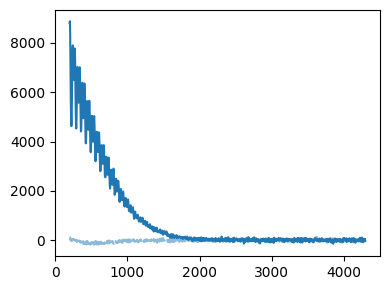
[10]:

_=tempo_eseem.plot()
../_images/notebooks_examples_77_0.png 
[11]:

tempo_eseem.pulse_program # this pulse program is supported, check the documentation for pulse programs which support worklfows

[11]:

'2P ESEEM'

[12]:

eseem_proc = tempo_eseem.workflow(zf=1024,verbose=True)

Starting ESEEM workflow...
Detected pulse program : 2P ESEEM
Baseline correction using an exponential decay function...
Applying Hamming window along dimension 1...
Zero filling 1024 points...
Generating frequency axes...
Fourier transformation...
Completed in 0.01 seconds.

[13]:

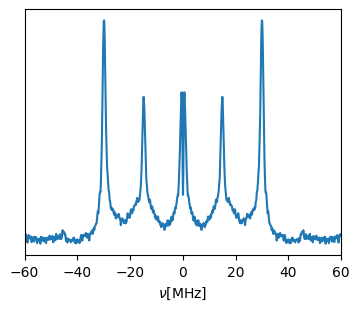
fig,ax = eseem_proc.plot()
ax.set_xlabel(r"$\nu$" + "[MHz]")
ax.set_xlim((-60,60))
_=ax.set_yticks([])
../_images/notebooks_examples_80_0.png